* "Fuzzy logic" has become a common buzzword in machine control. However, the term itself inspires a certain skepticism, sounding equivalent to "half-baked logic" or "bogus logic". Some other nomenclature might have been preferable, but it's too late now, and fuzzy logic is actually very straightforward. Fuzzy logic is a way of interfacing inherently analog processes, that move through a continuous range of values, to a digital computer, that likes to see things as well-defined discrete numeric values.
For example, consider an antilock braking system, directed by a microcontroller chip. The microcontroller has to make decisions based on brake temperature, speed, and other variables in the system.
The variable "temperature" in this system can be divided into a range of "states", such as: "cold", "cool", "moderate", "warm", "hot", "very hot". Defining the bounds of these states is a bit tricky. An arbitrary threshold might be set to divide "warm" from "hot", but this would result in a discontinuous change when the input value passed over that threshold.
The way around this is to make the states "fuzzy", that is, allow them to change gradually from one state to the next. You could define the input temperature states using "membership functions" such as the following:
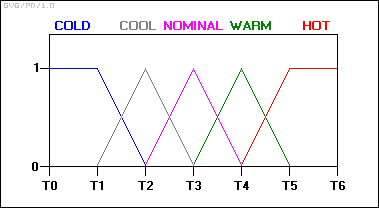
With this scheme, the input variable's state no longer jumps abruptly from one state to the next. Instead, as the temperature changes, it loses value in one membership function while gaining value in the next. At any one time, the "truth value" of the brake temperature will almost always be in some degree part of two membership functions: 0.6 nominal and 0.4 warm, or 0.7 nominal and 0.3 cool, and so on.
The input variables in a fuzzy control system are in general mapped into by sets of membership functions similar to this, known as "fuzzy sets". The process of converting a crisp input value to a fuzzy value is called "fuzzification".
A control system may also have various types of switch, or "ON-OFF", inputs along with its analog inputs, and such switch inputs of course will always have a truth value equal to either 1 or 0, but the scheme can deal with them as simplified fuzzy functions that are either one value or another.
Given "mappings" of input variables into membership functions and truth values, the microcontroller then makes decisions for what action to take based on a set of "rules", each of the form:
IF brake temperature IS warm AND speed IS not very fast
THEN brake pressure IS slightly decreased.
In this example, the two input variables are "brake temperature" and "speed" that have values defined as fuzzy sets. The output variable, "brake pressure", is also defined by a fuzzy set that can have values like "static", "slightly increased", "slightly decreased", and so on.
This rule by itself is very puzzling since it looks like it could be used without bothering with fuzzy logic, but remember the decision is based on a set of rules:
-
All the rules that apply are invoked, using the membership functions and truth values obtained from the inputs, to determine the result of the rule.
-
This result in turn will be mapped into a membership function and truth value controlling the output variable.
-
These results are combined to give a specific ("crisp") answer, the actual brake pressure, a procedure known as "defuzzification".
This combination of fuzzy operations and rule-based "inference" describes a "fuzzy expert system".
Traditional control systems are based on mathematical models in which the the control system is described using one or more differential equations that define the system response to its inputs. Such systems are often implemented as "proportional-integral-derivative (PID)" controllers. They are the products of decades of development and theoretical analysis, and are highly effective.
If PID and other traditional control systems are so well-developed, why bother with fuzzy control? It has some advantages. In many cases, the mathematical model of the control process may not exist, or may be too "expensive" in terms of computer processing power and memory, and a system based on empirical rules may be more effective.
Furthermore, fuzzy logic is well suited to low-cost implementations based on cheap sensors, low-resolution analog-to-digital converters, and 4-bit or 8-bit one-chip microcontroller chips. Such systems can be easily upgraded by adding new rules to improve performance or add new features. In many cases, fuzzy control can be used to improve existing traditional controller systems by adding an extra layer of intelligence to the current control method




